現代のTRIZ
アナトーリー・ギン「教育体制の大きな改革は避けられない」
このページでは、TRIZマスターであり「新しい時代の教育」研究室長としてTRIZの考え方に基づいた教育法の開発・普及を進めているアナトーリー・ギンの文章を、本人の承諾を得て翻訳し、紹介します。
このページで紹介するのは、これまでに紹介した資料(「TRIZによる教育」、「教育システムの矛盾」)に指摘されている教育の矛盾を解消するためにアナトーリーが提唱する新しい教育の大枠を紹介する資料です。
この論文には著作権があります。
日本語の翻訳の著作権はサイト管理者にあります。
無断転載は禁止いたします。
教育体制の大きな改革は避けられない
アナトーリー・ギン
教育の新しい機能とTRIZに基づく教育学
何を教えるべきでしょうか?
古来教育の基本的な機能は文化の再生産、世代から世代への文化の継承でした。文化とはある社会で受け入れられている行動様式、基本的な学問、日常の概念や世界観、問題を解決するために用いる技術や方法の総体です。毎朝顔を洗う習慣、刑法、チーズを作る技術、二次方程式の根についての「ヴィエタの公式」、これらはすべて文化の要素です。
現代の教育が直面する基本的な矛盾は教育が持つこの機能に関係するものです。人類の知識の蓄積が猛烈な速度で増加してゆくことと、それと比べて個人が知識を蓄積してゆく速度は遅いこととの間の矛盾です。人類の知識の総量は小さく見積もっても幾何級数的に増加しています。ところが教育の技術は実質的には大きく変化していませんから、人類の知識の総量の増加に対応するように個人の知識を増加させることはできません。それではどうしたら良いのでしょうか。
これまで教育の水準を高めるために方策として用いられてきた主な手段は拡大の道、つまり教育にかける時間を増やすことです。現代の教育学は教育の密度を高めるいくつかの方法を持ってはいます。しかし全体としていえば、こうした方法が問題を解決してくれるわけではありません。ところが、十分に効果的な(しかし、技術的にはまだ十分に検討されていない)アイデアが1つあります。個々の具体的な知識を教えることよりも優先してなによりも、すばやく、効果的に知識を獲得する方法(自ら学ぶ技能)を教えることです。このアイデアを教育技術として発展させること、これは現代の教育学の課題の1つです。この方向に向けて必要となる教育学上の発明の数は少なくありません。
しかし、21世紀の教育の内容的特徴となるべきもう1つの機能があります。これは20世紀における情報の爆発的増加によって生まれたものです。それがどんなことなのか、考えてみましょう。
有名な物理学者であるレオ・シラードがわかりやすい例をあげています。人類の知識の全てが1つの球だと考えてみましょう。そうすると、球の外側の空間は未知の領域です。球の表面は人類が持つ既知の知識と未知の部分との間の境界ということになります。すると球が大きければ大きいほど未知の部分に接する面積が大きくなることになります。また、表面上の点の一つひとつは新たな課題を意味します。
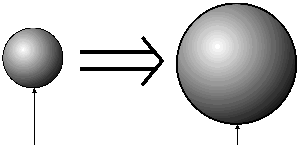
図1.未知と接する部分=新たな知識の部分
人々が直面する新たな課題の数は急速に増加しました。また、新たな課題を解決することがおよぼす影響の規模も拡大しました。課題を上手に解決できれば、新しい可能性が生まれます。逆に、下手な解決策は新しい問題を生じさせることにつながり、最悪の場合エコロジー上の大問題が発生することにもつながります。こうして、人類史上初めて、人類が直面する数多くの課題を上手に解決することを可能にするために、課題を解決する能力をもった大衆規模までの数の人材を育成するニーズが生じたのです。
「課題を解決することを職業とする人々が必要になる」と言うことができるでしょう。シラードに触れましたがこれは物理学に限った問題ではありません。工学、化学、生物学、心理学、社会学どれに限った問題でもありません。まさに、課題を解決する能力が求められているのです。なぜならば、現代という時代は社会のどのような専門分野にも収まりきれない、多様な要素を含む困難な課題に直面する機会がますます増えてゆく時代だからです。多様な要素を誰かが結びつけなくてはなりません。様々な専門分野の言語と利害関係とを理解することの出来る誰かが存在する必要があるのです。もし、創造的能力というものを学ぶことが可能であり、そこに何らかの法則性があるとしたら、誰かがそうした能力を使いこなすことができる。それが必要なのです。
本題を離れます。タイムマシーンが発明されたとしましょう。1人の中学生が乗り込んで13世紀のピサの大学にいって、当時のヨーロッパの大数学者が集まって大きな桁の割り算の問題を解く能力を競っているところに登場して競争に参加します。桁の大きい割り算の解を得るには長い経験と鋭い直感が必要とされ、大変難しい問題です。そもそも、数字はローマ数字で書かれています(アラビア数字がヨーロッパに伝わったのはこれよりも後のことです)。そして割り算を行うための方法というものが当時はそもそも存在しなかったのです。適当に答えを選んで検算をするというやり方を繰り返すだけでした。さて、この競争ではタイムマシーンの中学生が学者達に大差をつけて勝ってしまいます。この中学生は天才というわけではありません。単に「多項式の割り算」という方法を知っていただけのことです。
これがヒントになるかもしれません。すべての人を天才にするわけにはゆきません。しかし、多くの人に複雑な課題を解決する強力な方法を持たせるようにすることはできるのではないでしょうか。どうでしょう。
とりあえず1つの結論を整理しておきましょう。これまでは予測することさえ必要のなかった新しい課題と出会う場合に備えて準備をしておくこと。これは、科学技術革命の結果として必要になった、教育の2つ目の基本的機能です。しかも、今後はこの機能こそが教育に求められる主要な機能になると考えられます。
しかし、まだ難しい問題が残っています。高い課題解決能力を持った人々を育てることを目的とした教育コースはどう作ったらよいのでしょうか。そうしたコースの主な要件について考えてみましょう。
課題解決能力の育成
目標:経験のない課題に対処することのできる解決能力の高い思考とはどのようなものかを明らかにする。
この目標を達成するためには1つの教育学の体系を作り上げなくてはなりません。その教育学の体系を私達はTRIZに基づく教育学と名付けています。TRIZに基づく教育学の主な要素は次の表に示すものです。
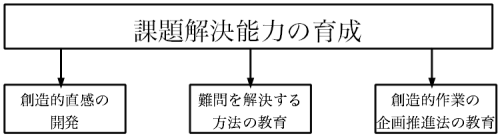
図2.
各要素について少し具体的に補足します。
I. 創造的直感の開発
ロシアの有名な航空機設計者で科学アカデミー会員のツポレフ博士は設計図を見ただけでその飛行機の良し悪しを判断することができたといいます。
直感はたくさんの課題を解決することによって開発されます。課題解決能力に求められる創造的直感は、教育コースの中で創造的思考を求められる学習課題と数多く取り組むことによって育てられます。
II. 難問を解決する方法の教育
TRIZに基づく教育学は当然TRIZの歴史の中で開発されてきた方法を軸としています。固定観念を取り除くための手法、矛盾を解決するための方法、難問を解決するための手順その他のTRIZの課題解決ツールです。同時に、TRIZに基づく教育学はこれ以外の方法も忘れているわけではなく、補助的な手段として取り入れています。
TRIZに基づく教育学には就学前の児童から始まって大学生や社会人に至るまで様々な年齢層を対象として難問を解決する方法を教えてきた経験の蓄積があります。各年齢層に対応した説明用の例や学習用の課題の蓄積もあります。創造的な活動を行うための特殊な方法を習得するためには主として次の能力を特徴とする強靭な思考力を形成しておくことが求められます:
- 大量の事実の中から法則性を抽出すること
- モノや現象の中に明示的でない特性、つまり課題を解決する上で利用することのできる資源を発見すること
- その都度の状況で必要とされる細部を含めて原因・結果の関係を整理すること
- 知識の量が十分でない状況で形式論理を使いこなすこと
- 状況の中で重要な点は何か見分けること、問題の核心を明らかにしてくれる質問を投げかけること(人に対して、あるいは自然を対象として——この場合には実験の計画を立てることになります)
- (意識的に)仮説を立てて、それを検証する仕組みを企画すること
- 矛盾に対処すること
- 広い領域にまたがる様々な種類の類比を自由に使うこと
- 様々な種類の層別・分類を行うこと
III. 創造的作業の企画・推進方法の教育
非常に才能がある人が一生かけて何も成し遂げられないことがあります。エチュードを懸命に練習しなければ名手と呼ばれる演奏家になることはできません。自分の作業を上手に企画・推進できなければ、難問に取り組んで良い結果を出せるようになりません。
知的作業を企画・推進することには次の各項目が含まれます:
- 作業の計画を立てること
- 情報に基づいて作業を進めること。自分用の情報データベースを構築することも含まれます
- 有効な参照を行うこと
- 素早くノートを取ること、情報の内容をうまく表現した記号(イメージ)にまとめること
- 速読
- 自分の時間の管理
- など
集団で知的活動を行う際に求められる次のようなプロジェクト・マネージメントの能力も同じく重要です。
- 議論を建設的に進めて、そこからの帰結を正確に導きだす能力
- 自分が達成したことを口頭あるいは文面で説明する能力
- 同僚(他の参加者)の作業結果を編集し、評価し、補足する能力
- その他
まとめ
西暦三千年紀が始まる前後から、17–18世紀に成熟期を迎えた旧来からの教育手法は「空回り」をしはじめました。この現実の本質を理解して時代の要請に遅れをとらないようにしたいと思います。皆さんのご賛同を期待しています。
